分形及其音频可视化应用呈现

发表于 2023-06-10 更新于 2023-07-28 分类于互动媒体技术本文字数： 2.3k 阅读时长 ≈ 8 分钟

整理了本科一些小demo的文档。

这次实验学习G站上一位大佬的作品，自己也尝试着将音频数据可视化与分形图形整合了一下。

实现目标：

读取音频数据到缓存，考虑用分析声音的音调，让音调和颜色对应起来。

给简单的分形图形添加填充颜色，构成更和谐一点的音乐可视化的动画。

一.效果展示：

使用随机噪声，并使颜色均匀变化生成分形的变换效果：

读取音频数据，“李克勤 - 月半小夜曲 (清唱版).mp3”的前奏部分及清唱部分效果展示：

二.可视化处理：

1.音频信号处理：

处理音频信号可以用processing的sound库或是minim库。这里用到的是minim库，我依照一般音频处理的核心流程制作了一个简单的图表，如下所示。

我对照着minim库官网的文档我对一些函数的作用进行了标注，并分析了代码作用。

1
2

fft = new FFT(bufferSize, sampleRate);    //快速傅里叶变换将时域上的数据流转换到频域
fft.logAverages(fft_base_freq, fft_band_per_oct); //两种方法将信号按频率划分成不同的band以方便后续的分析

1）fft.logAverages

1	fft.logAverages(fft_base_freq, fft_band_per_oct);

组成音频的信号的频率的范围取值从1到几万(e.g. 44100 Hz)不等（这个说法不严谨但暂这么认为），但要实时地分析几万个信号不太高效，而Minim提供了两种方法将信号按频率划分成不同的band以方便后续的分析，分别是：linAverages和logAverages，顾名思义，线性的和对数的。
这里我使用了对数方法对频率进行划分。

2）fft.window(FFT.HAMMING)

频率划分完毕以后，我们需要对音频信号进行加窗，也就是一次仅处理窗中的数据。因为实际的语音信号是很长的，我们不能也不必对非常长的数据进行一次性处理。明智的解决办法就是每次取一段数据，进行分析，然后再取下一段数据，再进行分析。

这里使用Hamming方法加窗。

关于Hamming窗口：

怎么仅取一段数据呢？一种方式就是构造一个函数。这个函数在某一区间有非零值，而在其余区间皆为0.汉明窗就是这样的一种函数。它主要部分的形状像sin（x）在0到pi区间的形状，而其余部分都是0.这样的函数乘上其他任何一个函数f，f只有一部分有非零值。

为什么汉明窗这样取呢？因为之后我们会对汉明窗中的数据进行FFT，它假设一个窗内的信号是代表一个周期的信号。（也就是说窗的左端和右端应该大致能连在一起）而通常一小段音频数据没有明显的周期性，加上汉明窗后，数据形状就有点周期的感觉了。

3）fft.forward( )

调用FFT对象的forward函数，得到频域结果以后就可以开始分析了。官网给出了示例代码写的很清楚，它提供的可视化就是一个循环取出每一个band的amplitude，然后将其映射到矩形的高度上。它提供的可视化就是一个循环取出每一个band的amplitude，然后将其映射到矩形的高度上。

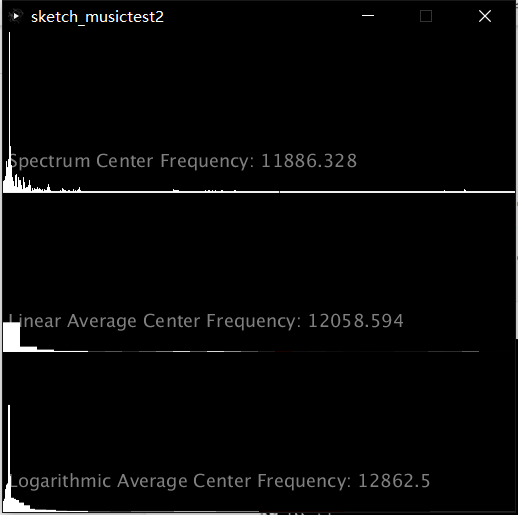
官网示例程序：

我截取官网给出来的一段示例代码，试图分析出它的意图。下面代码对应的正好是图片中Linear Average Center Frequency部分的绘制：

int w = int( width/fftLin.avgSize() ); 
for(int i = 0; i < fftLin.avgSize(); i++)
{  //遍历fft频率分段的每一个频率段，只要有变换就会有avgSize
   // if the mouse is inside the bounds of this average,
   // print the center frequency and fill in the rectangle with red
   if ( mouseX >= i*w && mouseX < i*w + w )
   {  //获取这个频率段的中位数？（频率）
      centerFrequency = fftLin.getAverageCenterFrequency(i);
      fill(255, 128); 
      text("Linear Average Center Frequency: " + centerFrequency, 5, height23 - 25); 
      fill(255, 0, 0); //简单的鼠标悬浮交互，换颜色
   }
   else
   {
       fill(255);
   }
   // draw a rectangle for each average, multiply the value by       spectrumScale so we can see it better
   rect(i*w, height23, i*w + w, height23 - fftLin.getAvg(i)*spectrumScale);
}

2.分形图像处理：

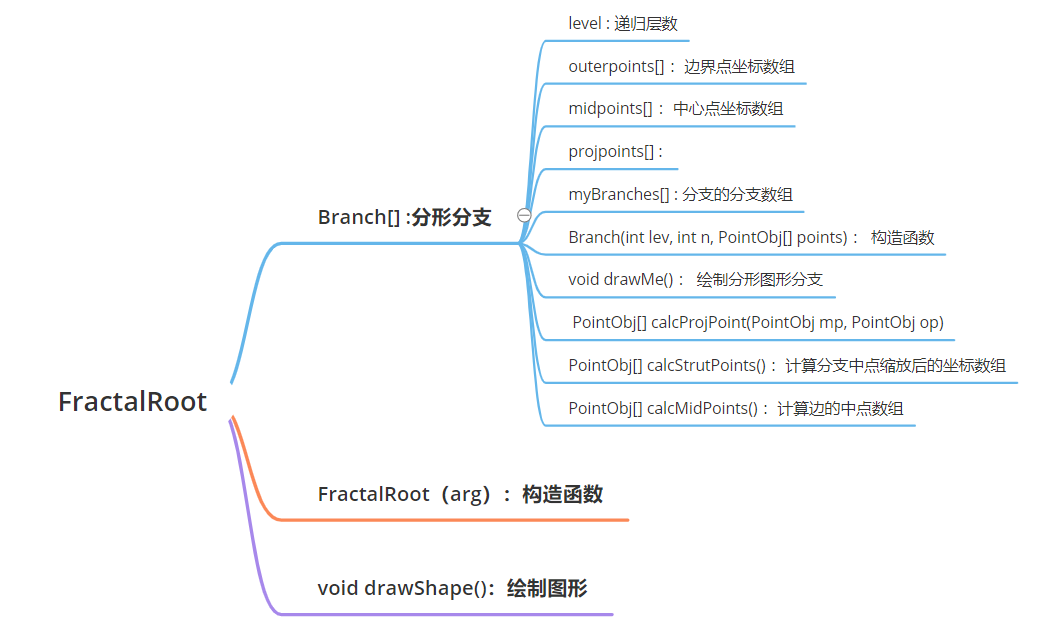
绘制分形图像的核心在于递归这一部分的代码，而优化可视化的效果在于改善每一个分支的结构。我希望能够计算一个多边形的每个分支的坐标点，就需要先得到原多边形的边界点坐标，每条边中点的坐标，剩下两个点需要根据多边形的边数和分支中心点设定相对应的函数进行计算。

下面我挑选了相对简单的正方形画了个示意图。

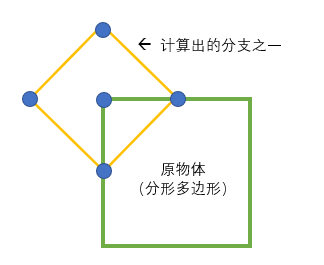
下面是关于分支对应坐标点计算的代码部分，计算完分支点需要的外围坐标后把计算出的这些坐标数据全部传输给子分支。

outerPoints = points;
midPoints = calcMidPoints();
projPoints = calcStrutPoints();
   
 if ((level+1) < _maxlevels) {
      Branch childBranch = new Branch(level+1, 0, projPoints);
      myBranches = (Branch[])append(myBranches, childBranch);

      for (int k = 0; k < outerPoints.length; k++) {
        int nextk = k-1;
        if (nextk < 0) { 
          nextk += outerPoints.length;
        }
        PointObj[] newPoints = {  //分支的外围坐标点包括下面的类别
          projPoints[k], midPoints[k], outerPoints[k], midPoints[nextk], projPoints[nextk]
        };
        childBranch = new Branch(level+1, k+1, newPoints);
        myBranches = (Branch[])append(myBranches, childBranch);//子分支
      }
    }

使用vertex函数递归的对每个分支进行绘制。

void drawMe() {
  strokeWeight(4 - level); 
  beginShape();
  for (int i = 0; i < outerPoints.length; i++) {
    int nexti = i+1;
    if (nexti == outerPoints.length) { 
      nexti = 0;
    }
    vertex(outerPoints[i].x, outerPoints[i].y);
  }
  endShape(CLOSE);
  for (int k = 0; k < myBranches.length; k++) {
    myBranches[k].drawMe(); //递归绘制分形分支
  }
}

三.优化处理：

以上，理解了这个库的相关用法，我个人感觉显示出的图表中是能反应出声音的振幅（响度）和频率信息的。可以根据计算当前所有频率段的幅值均值象征此时音量的响度，同时再根据各个频段的声音的幅值大小，逐频段对我的分形图形进行不同的效果变换。

需要注意的是：以下频段 i 都是简写，实际操作是需要依次计算边界值频率的！没有确切的频率区间数据就没有办法对每个区间的数据进行个性化处理。

只列出我在第一个区段的处理代码：

//根据频段分组的可视化处理
// 0 ***** 0 Hz - 86 Hz ***** //
// 这一部分是极低频部分，人是发不出的这样的声音的
int i = 0;
_b = round(drawFreqArr[i] * 255);  //超低频部分能够影响颜色中的蓝
if (_b < 50) {
  _b = 50;
}

一点自己的理解：

音乐踩点：

当某一个频段的幅值突然变得很大时，有可能此处正是这首曲子边奏的一个节点或是曲子的一个节奏点之一，这个时候可以考虑让分形效果出现一些比较明显的变化（比如说边长增加，多边形边数+1等等）让我们的可视化图像能够更好的“踩点”。

音调变换可视化：

而对于一个hamming窗口内不同频率区段的声音，我们也可以分别赋予其一定的权值，调整填充及画笔颜色的r g b值，这样就可以使在某一时刻听到的声音较尖锐时，分形图像颜色偏红调，听到的声音较低沉时，分形图像颜色偏蓝调。

响度可视化：

通过计算hamming窗口内不同频率区段幅度的均值，我们大致是可以确定这个时刻音频的响度大小并将其可视化的。

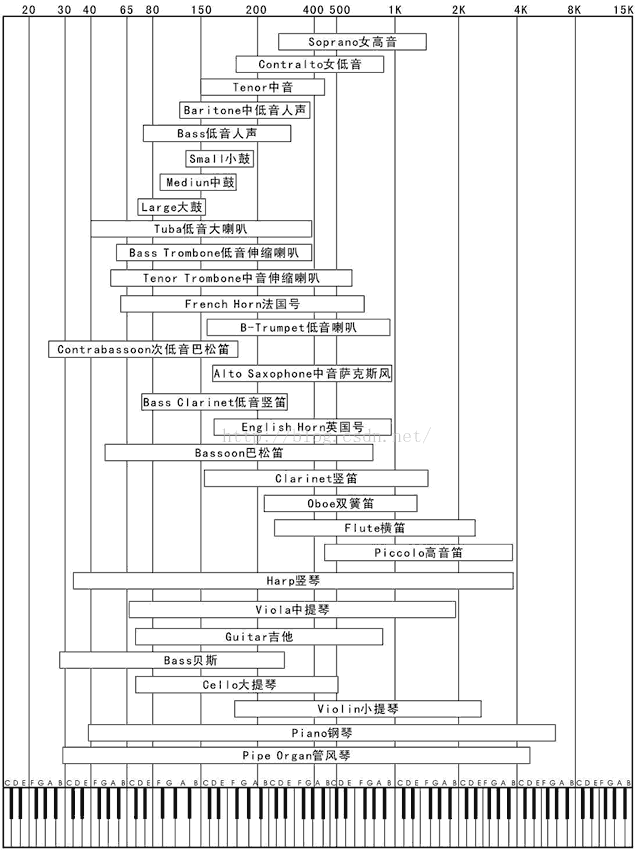
我查阅了些资料，找到了一个人声以及常见乐器声对应频率的表格（如下），然后如上面的图所示挑选了一部分区段进行处理，发现其实效果不错。