细胞自动机
整理了本科一些小demo的文档。
一.实验选题:
- 自己实现一种细胞自动机,用excel或任意编程方式,可尝试在以下方面进行拓展:
- 网格结构(六边形/其他形态)
- 邻域
- 计算规则
- 数值形式(标量/矢量/张量…)
- 可视化方式(静态/非静态)
- 其他
二.实验过程:
在网格结构为正方形细胞自动机的基础上,我尝试着使用matlab制作了一个网格结构为正六边形的细胞自动机。
- 绘制正六边形蜂窝网络:
要实现网格结构为正六边形的细胞自动机,首先先要绘制出正六边形蜂窝网络,这涉及到了一定的算法实现。
实现网格结构为正六边形的细胞自动机的状态转移,运算过程中需要记录储存的数据有:
1.细胞状态:0或1 ( 0代表生存,1代表死亡 )
2.细胞中心坐标:(x0, y0)
3.细胞六个边界点的坐标:(xi, yi) (i=1,2,3,4,5,6)
4.六个邻近细胞行、列号:( row, col )
考虑到以上数值都是整型或是浮点型数值,我选择用数组这一数据结构对其进行处理。
下面的过程记录会对这些数据的处理按顺序进行简单的介绍。
1 六边形网络算法简单介绍:
对于正方形来说,要构成一个网格,我们只有一种方式,但是对于正六边形来说,我们有多种方式排列,如下图所示的有边朝上的flat topped和尖朝上的pointy topped基础形式。
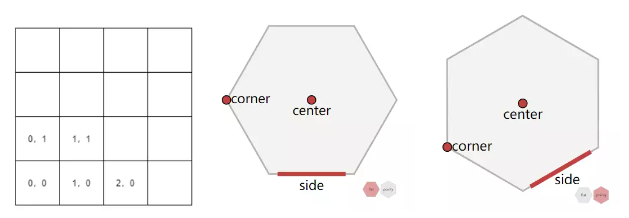
而在边朝上flat topped和尖朝上的pointy topped这两种排列的基础上,又可以拓展出以下偏移坐标系。
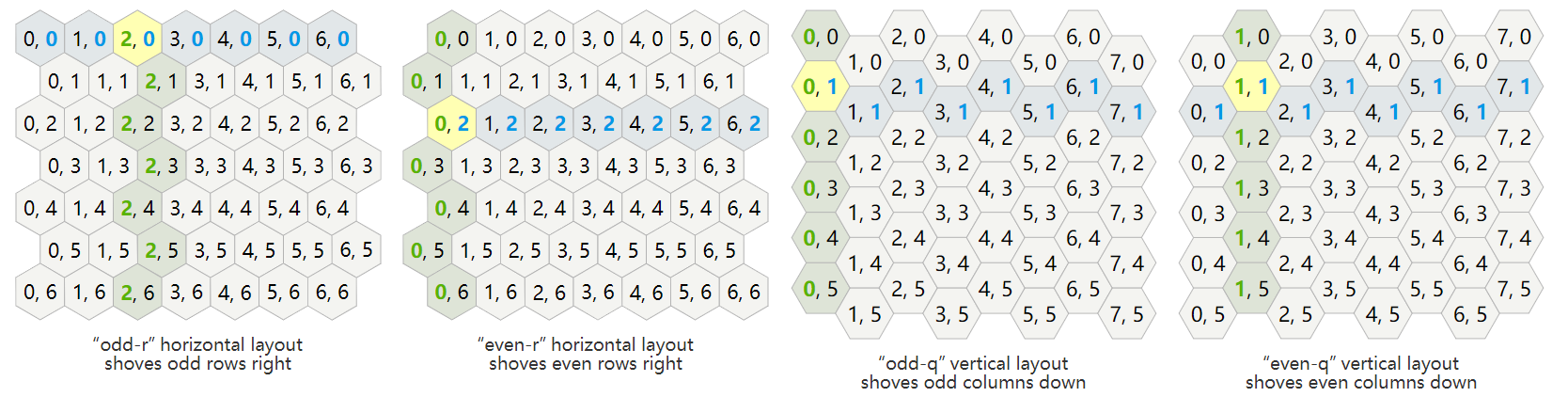
在偏移坐标系中,最常见的方法是将每一行(或列)进行偏移。每一列被命名为col(q),每一行被称为row®。如上图所示,我们可以选择偏移奇数行或者偶数行,也可以选择偏移奇数列或者偶数列。
2 中心center点绘制:
正六边形网络的排列具有高度的规律性,在绘制网络之前,我们可以先推算出每个正六边形的中心点位置并画出,然后再根据中心点绘制完整的正六边形。
a 中心点初始化
首先我们设置正六边形的边长为1/2,如下图所示,左侧第一个正六边形的横坐标初始值可以设定为:0.5或1.25。
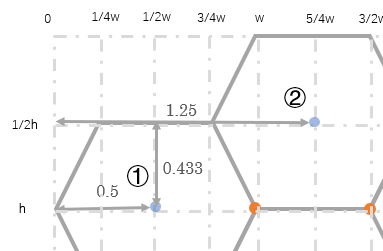
b 位置推演
如下图所示,正六边形的边长不变,水平方向上中心点到下一个中心点的横纵坐标变化为:
水平方向上:$$x_{next}=x_{recent}+\frac{3}{2}$$
垂直方向上:$$y_{next}=y_{recent}+\frac{\sqrt{3}}{4}$$
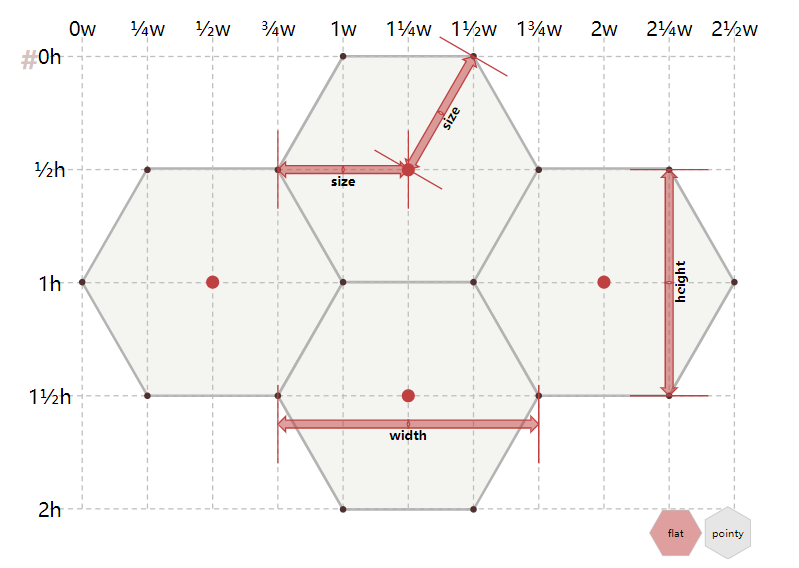
完成初始化和确定好推演规则以后,就可以编写代码先绘制出六边形网络的所有中心点了,如下图所示。

3 六个边界点坐标计算:
这里采用了flat topped类型的正六边形布局。
如下图所示,设置正六边形的边长为1/2,设正六边形的中心点坐标为(x,y),则它的六个边界点的计算如下图标注所示:
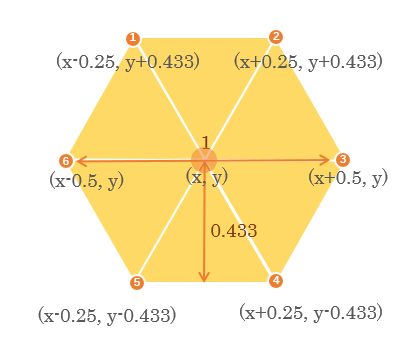
根据上一个步骤推演计算得到的中心点坐标,计算得出正六边形六个边界点坐标值,并且调用一下matlab中的patch函数进行多边形绘制:
1 | patch(reshape(Cell(i,j,3:8,1),[1,6]),reshape(Cell(i,j,3:8,2),[1,6]),'w','EdgeColor','blue' ); |
效果如下图所示:
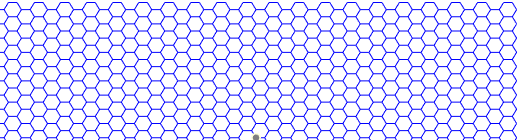
至此基础的绘图完成,但是我们还需要给每一个正六边形的位置进行行列编号处理,对于边界的正六边形还需要将其设置为非细胞。
4 行列编号:
a 排除非细胞点(边界点):
由于设定规则需要获得一个细胞周围细胞的状态,所以我们需要在整个界面边界设置一圈“非细胞”,以免计算时出现越界的情况。
对于下图网格的每个交点进行遍历,搜索该交点附近的2个网格的交点,并计算两个点之间的距离。当距离值符合一定限制时。如图所示的浅蓝色圆形为有效搜索范围,计算出大致的范围半径并判断当前正在搜索的正六边形的中心坐标是否在范围内。如果改正六边形周边六个相邻位置都有正六边形,那么它是细胞,反之不是。
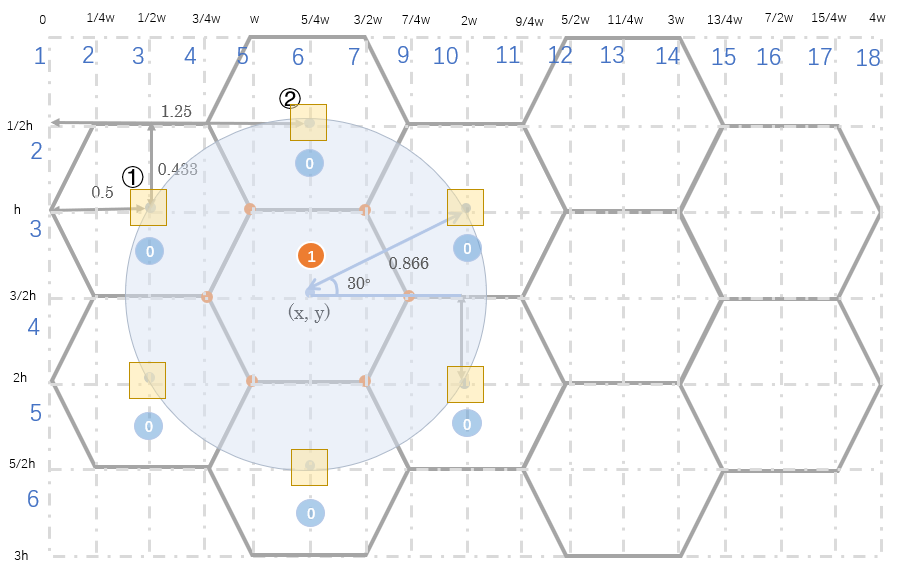
部分判断代码:
1 | %黄色区域范围计算 |
b 行列号初始化设置:
如上图所示,在确定交点为正六边形中心点,调用循环遍历的过程中,把判定为细胞的六边形的行列号一同进行标注即可。
修改正六边形的边长大小,已达到连续状态的细胞自动机可视化。
- 规则设定:
每个细胞有两种状态-存活或死亡,每个细胞与以自身为中心的周围六格细胞产生互动。
最基础的生存游戏设定的演变规则如下表所示:
1 基础生命游戏规则:
| 条件 | 状态转变 | 模拟依据 |
|---|---|---|
| 当前细胞为存活状态时,周围低于2个存活细胞时 | 细胞变成死亡状态 | 模拟生命数量稀少 |
| 当前细胞为存活状态时,周围有2/3个存活细胞时 | 细胞保持原样 | - |
| 当前细胞为存活状态时,周围有3个以上的存活细胞时 | 细胞变成死亡状态 | 模拟生命数量过多 |
| 当前细胞为死亡状态时,当周围有3个存活细胞时 | 细胞变成存活状态 | 模拟繁殖 |
规则设定代码实现:
1 | % 演变部分代码 |
按照以上规则进行随机初始化后,运行细胞自动机,最终的结果会演化呈现出几种稳定的结构:

2 规则变更-扩散效果:
规则设定:先把中间点置为1,每一时间步对每一点,如果周围六个点之和为偶数,则变为0,为奇数则变为 1。
规则设定代码实现:
1 | % 演变部分代码 |
按照以上规则进行初始化赋值设置中心点为1,运行细胞自动机,得到如下所示的效果:

仔细观察其实也可以发现这就是分形效果的一种演变。更改初始化点的位置,可以获得不一样的效果实现,如图蓝色为初始化四个边界点为状态1的单独效果,黄色为累积叠加效果:


3 规则变更-连续状态:
更改了一下每个细胞中存储的状态值,现在细胞中存储的不仅仅是0或1任意一个整数值,而是0-1的任意一个浮点数数值了。
下面设计了一个比较随意的规则,缩小网格数便于调试与观察。
1 | if N_live>5 |
研究了好久Matlab官网的colormap函数,终于弄明白了这个函数的机制,自己写了一下不同数值映射到colormap的颜色上的代码:(只用了10种颜色,颜色太多网格数也太多展示效果也不明显。)
1 | color = colormap(bone(10)); %颜色映射 |
测试效果如下所示:

三.实验结果展示:
基于以上的操作,自己对细胞自动机的规则设定和初始化进行了很多尝试,并且又挑选出了一些规律性强一点的变化进行展示:


挑选了一些状态值为连续的细胞自动机颜色变化的生成图出来(无聊的小李玩了半天= =):


想到小律老师上课讲过的热传导示例程序,我决定改一下规则实现一下,尝试了以下的模板。
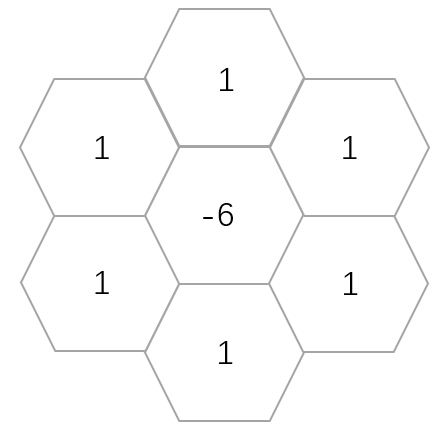
mark一下关键规则设定代码:
1 | changed=Cell( i, j, 1, 1)*(-6)*delta; |
实现效果(左边是过程动图,右边是最后的结果):
(好鲜艳,眼睛快被闪瞎了)
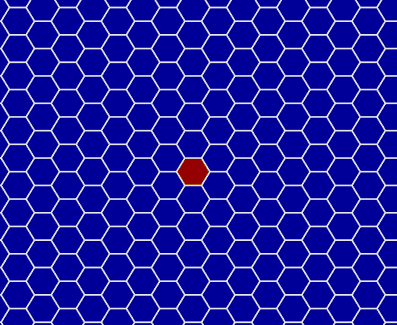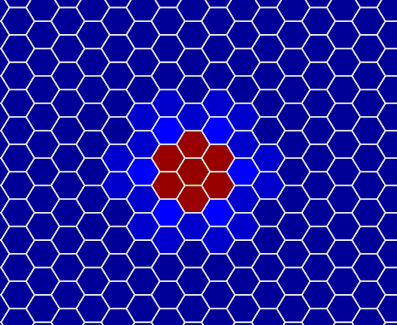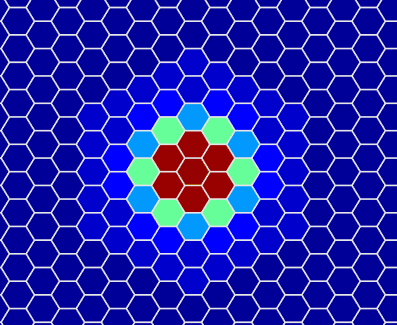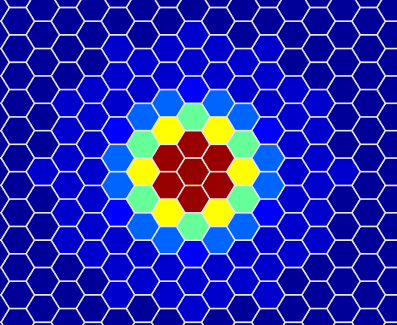

修改delta来个加速变化 ( =v= )!
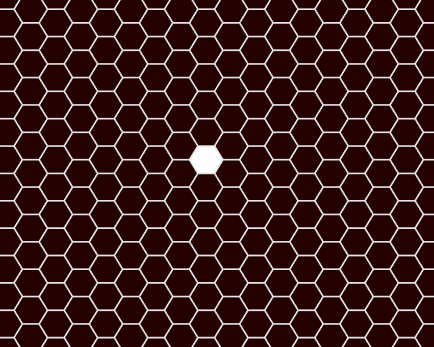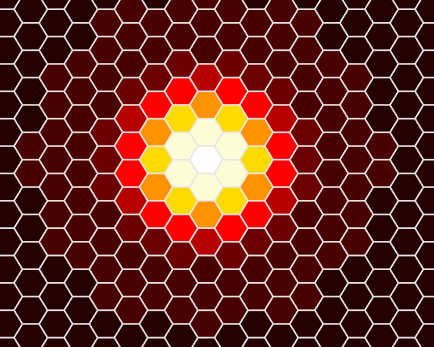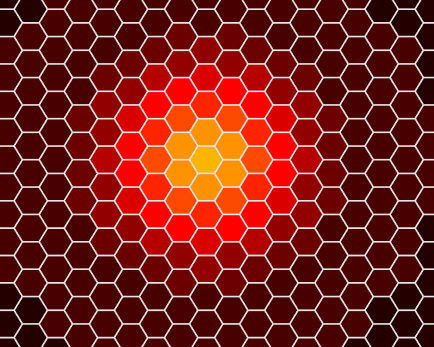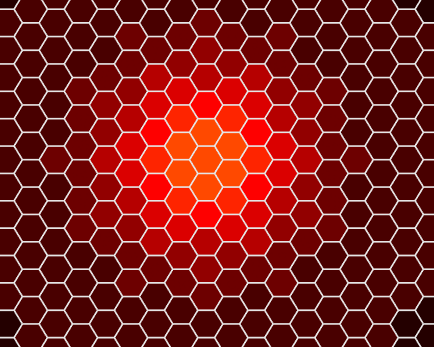
真好玩,收工!