Shader数学基础

发表于 更新于 分类于 本文字数： 3.1k 阅读时长 ≈ 11 分钟

Shader数学基础

1. 笛卡尔坐标系

二维坐标系OpenGL的原点在屏幕左下方，而DX的原点在屏幕左上方。

  1. 相关概念
    1. 基矢量：坐标系的三个坐标轴；
    2. 标准正交基：三个坐标轴相互垂直，长度为1；
    3. 正交基：相互垂直但长度不为1；
    4. 左手坐标系/右手坐标系：拇指x，食指y，中指z；
    5. 在Unity中，模型空间使用的是左手坐标系，观察空间使用的是右手坐标系；

2. 点和矢量

  1. 相关概念

    1. 点：代表n维空间中的一个位置；
    2. 矢量：包含模和方向；通常被用于表示相对于某个点的偏移；
    3. 矢量点积（内积）：点积是把两个矢量对应分量相乘后再取和，最后结果是标量；点积的几何意义是投影；a点乘b相当于计算b在a方向上的投影，然后在乘上a的模；
    4. 矢量叉积（外积）：叉积的结果是矢量； |axb|=|a||b|Sinθ；平行四边形面积；常应用于计算垂直于一个平面，三角形的矢量，判断三角形面片的朝向；
    5. 叉积相关计算公式👇：

    叉积（向量积、外积）的运算法则及其与点积（数量积、内积）的混合运算_叉积计算公式_zeeq_的博客-CSDN博客

3. 矩阵

  1. 相关概念
    1. 方块矩阵：行列数目相等；
    2. 对角矩阵：除了对角线外其余所有元素为0；
    3. 单位矩阵I：对角矩阵，且对角线元素为1；
    4. 转置矩阵：对原矩阵进行转置运算；(AB)T=BTAT;
    5. 逆矩阵：如果有一个逆矩阵，则这个矩阵可逆；矩阵的行列式不为0，则该矩阵可逆；MM-1=M-1M=I；（M-1）T=（MT）-1; (AB)-1=B-1A-1;
    6. 正交矩阵：一个矩阵和它的转置矩阵的乘积是单位矩阵；M-1=MT；正交矩阵的每一行都应该是单位矢量，这样它们与自己的乘积才能为1，且行彼此之间相互垂直，这样与彼此的乘积才能为0；
    7. 正交基：一组基矢量之间相互垂直；
    8. 标准正交基：满足正交基的情况下矢量的模为1；
    9. 行矩阵/列矩阵：矩阵乘法次序对运算复杂度有影响，矩阵乘法不满足交换律，在Unity中一般都把矢量放在矩阵的右侧，把矢量转换成列矩阵来运算；
  2. 矩阵变换的几何意义

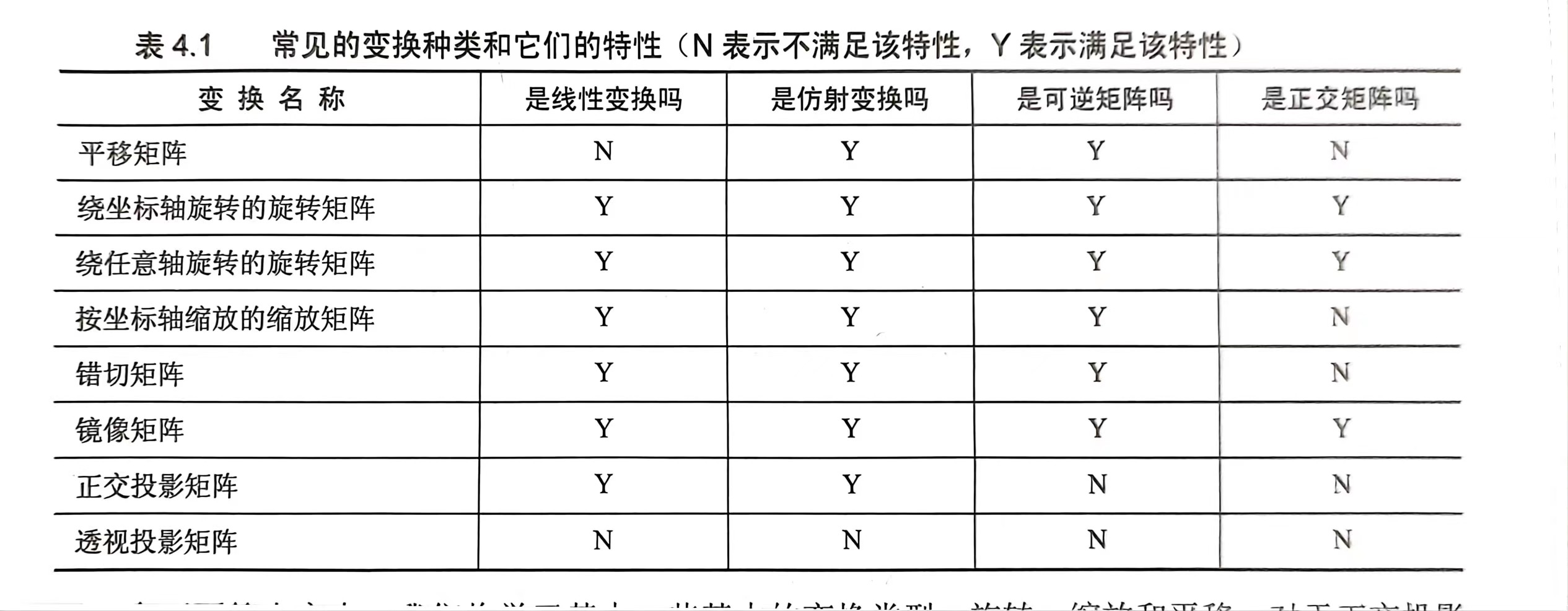
    1. 线性变换：缩放，旋转，错切，镜像，正交投影；

    2. 仿射变换：线性变换+平移变换；可以使用4x4矩阵来表示，需要把矢量拓展到四维空间下，也就是齐次坐标空间 ;

    3. 齐次坐标：四维矢量，点的w为1，向量的w为0；对于一个点，平移，缩放，旋转效果都能够施加上，然而对于方向向量，平移的效果就会被忽略；

      Image

    4. 复合变换：缩放-旋转-平移；

      1. 变换的次序不同，得到的变化结果也是不同的；
      2. 旋转变化：unity中的旋转变化默认是zxy变化，即按照坐标系E的z，y，x轴进行变化；

4. 坐标空间

Image

  1. 相关概念

    1. 定义坐标空间需要一个原点和三个坐标轴方向，而这是基于另一个坐标空间的，即每个坐标空间都是另一个坐标空间的子空间；

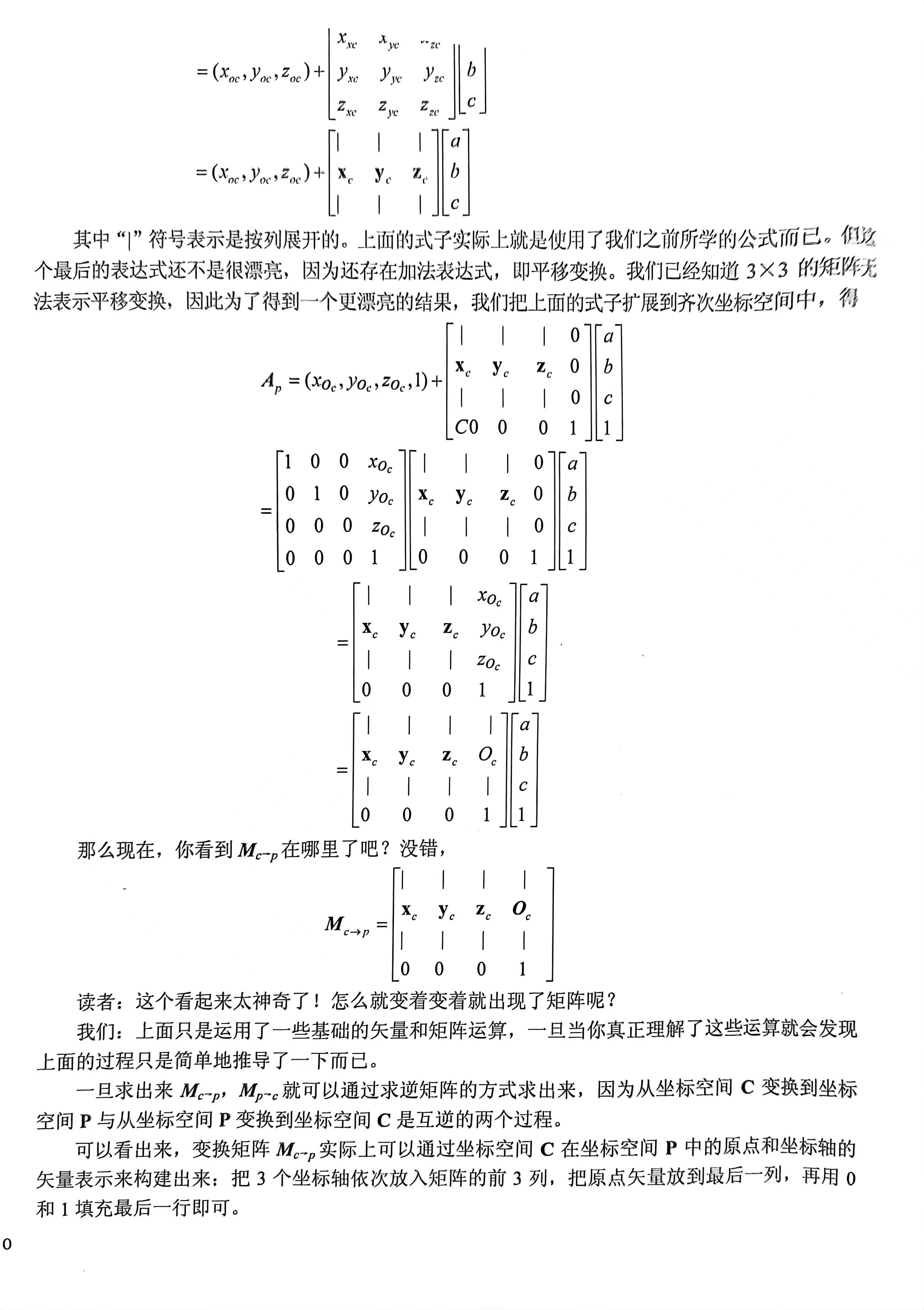
    2. 子坐标空间c到父坐标空间p的转换计算可以总结为：

      Image

    3. 对矢量的坐标空间变换可以仅用3x3矩阵表示，因为矢量是没有位置的不需要平移变换；unity中经常使用变换矩阵的前三行前三列来对法线方向，光照方向进行空间变化；

    4. 如果变换矩阵Mcp正交，那么可以由其转置直接获得Mpc，进而获得xp，yp，zp向量；即在矩阵中读取列表示前一个坐标空间的方向轴，读取行表示后一个坐标空间的方向轴；

      Image

    5. 模型空间：unity的模型空间是左手坐标系；由美术人员在建模软件中确定好位置；

    6. 世界空间：unity通过transform修改position改变模型的位置，位置值是相对transform父节点的，如果没有父节点，则位置为世界坐标系中的位置；

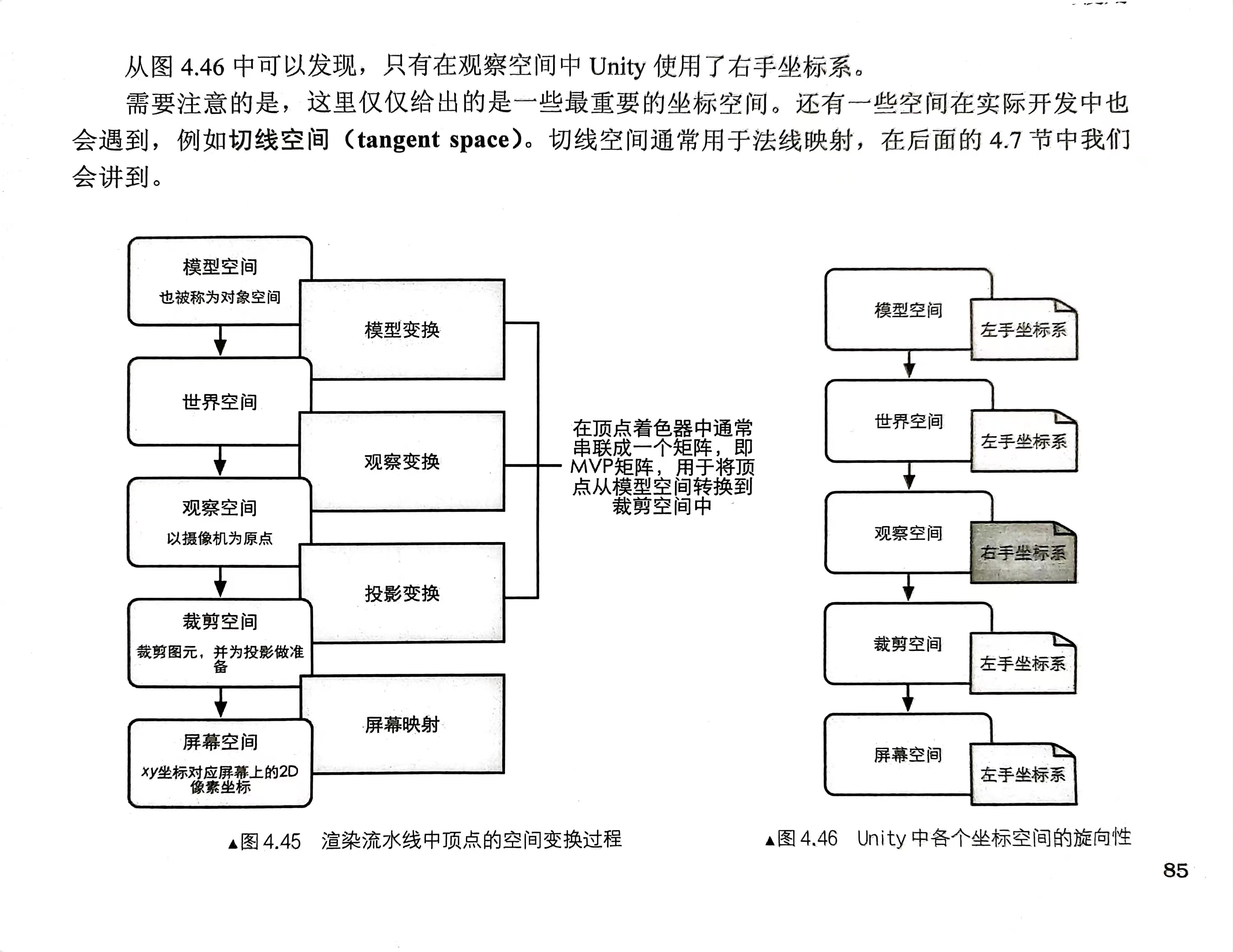
    7. 观察空间：不同于屏幕空间的二维，观察空间是一个三维空间，unity在观察空间中使用右手坐标系，这也是符合OpenGL传统的，摄像机的正前方指向的是-z方向；

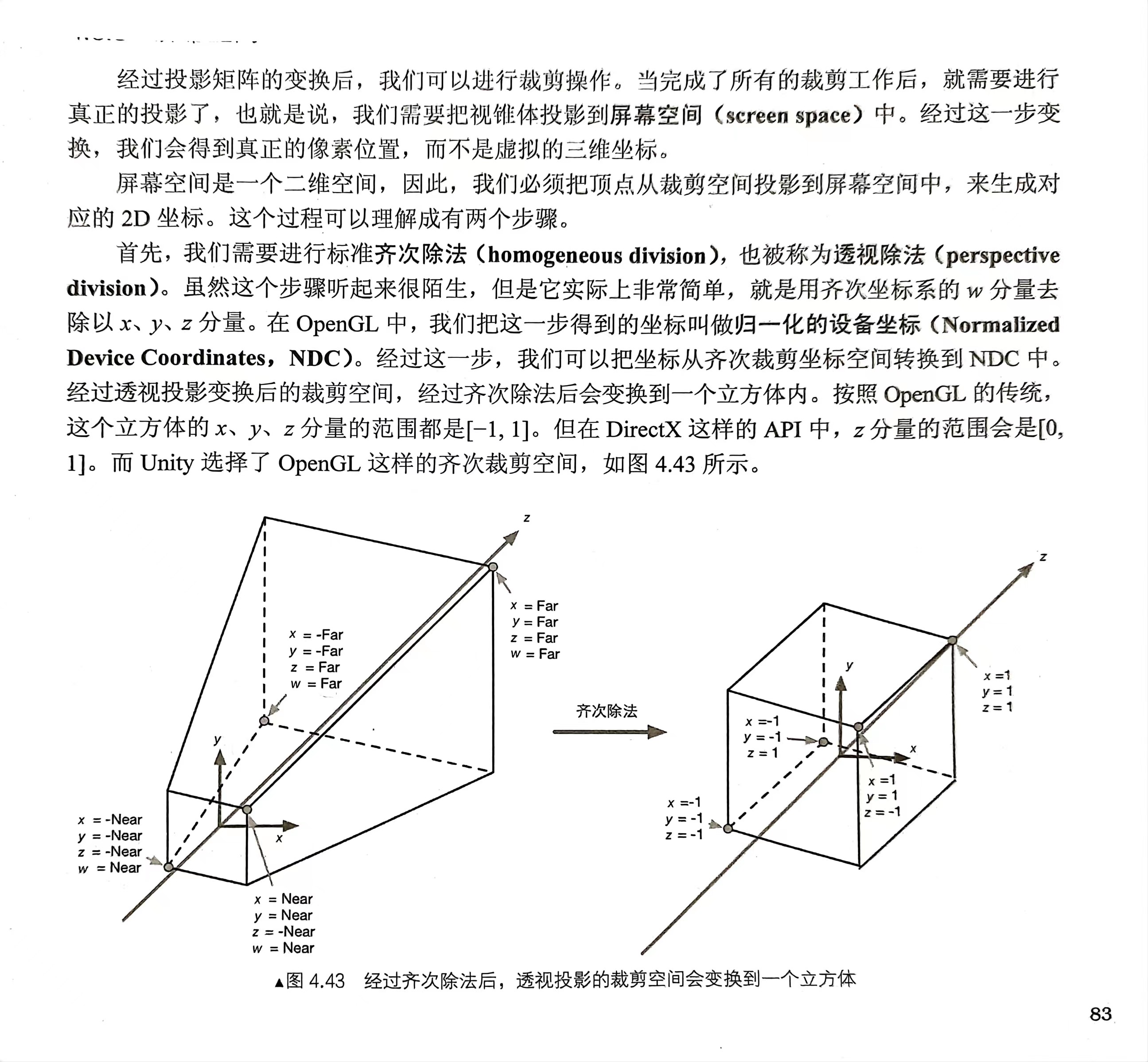
    8. 裁剪空间：也称齐次裁剪空间，位于裁剪空间内的图元会被保留，为投影操作进行准备，视锥体有正交投影和透视投影两种；在unity中，裁剪空间到屏幕空间是unity直接帮忙完成的，所以unity中只需要把模型空间转到裁剪空间即可；

    9. **屏幕空间：**完成裁剪工作之后，需要把视锥体投影到屏幕空间，经过投影，可以获得真正的像素位置，而不是虚拟的三维坐标；使用透视除法（xyz/w）获得标准设备坐标NDC，在OpenGL中，xyz范围都为-1到1，而在DX中，z的范围是0到1；

      Image

    10. 模型变换：模型空间→世界空间；

    11. 观察变换：世界空间→观察空间；观察相机在世界坐标系中的变化，进行逆变换后对z坐标进行取反操作即可获得变换矩阵；

    12. 透视投影变换：投影变换没有真正的进行投影，而是为投影做准备，透视投影将相机空间中的点从视锥体(frustum)变换到规则观察体(Canonical View Volume)中（对xyz分量进行了不同程度的缩放，z坐标还做了平移变换）。投影变换以后如果顶点在视锥体内，则其坐标必须满足：-w ≤ x/y/z ≤ w;

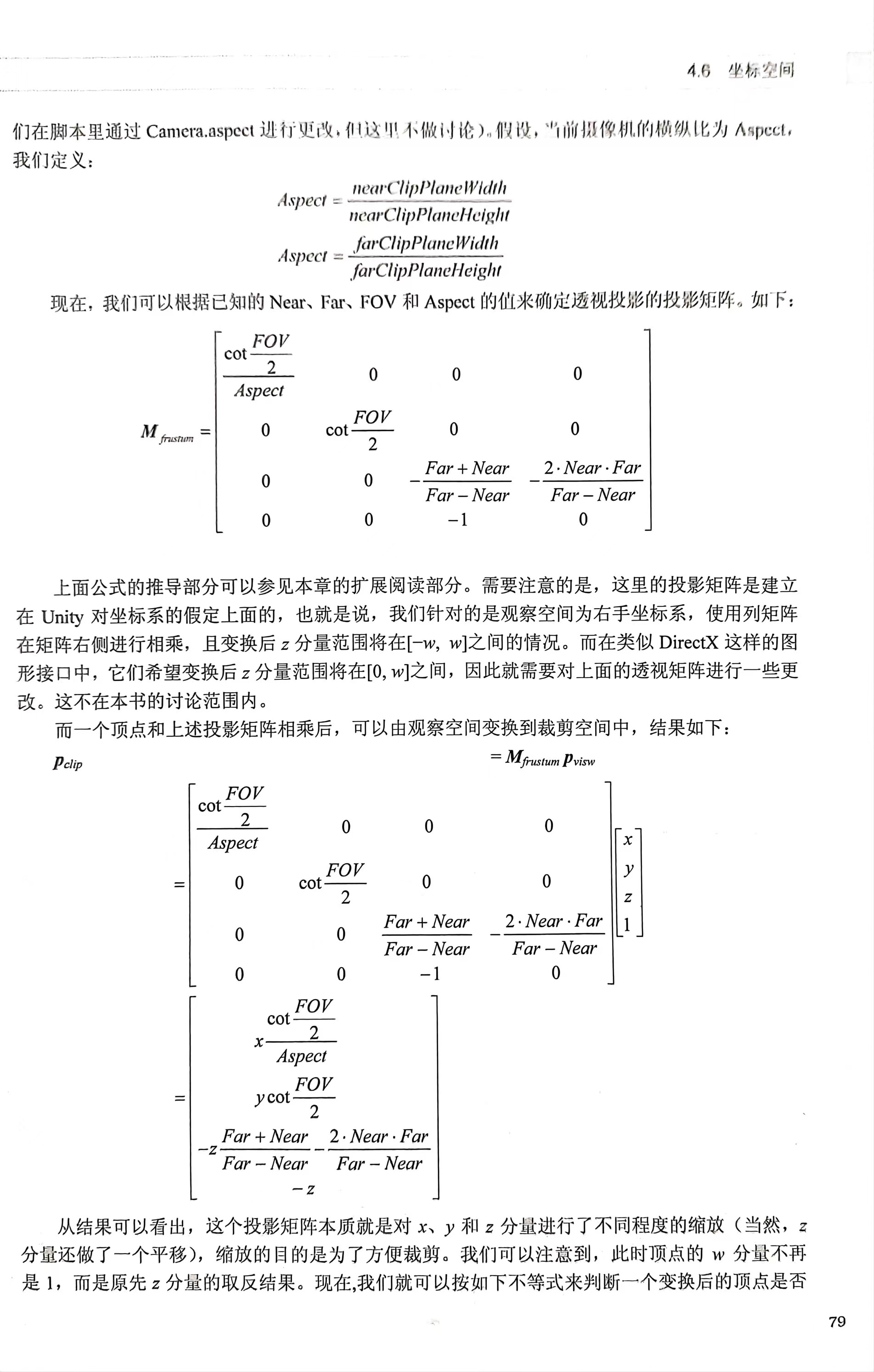
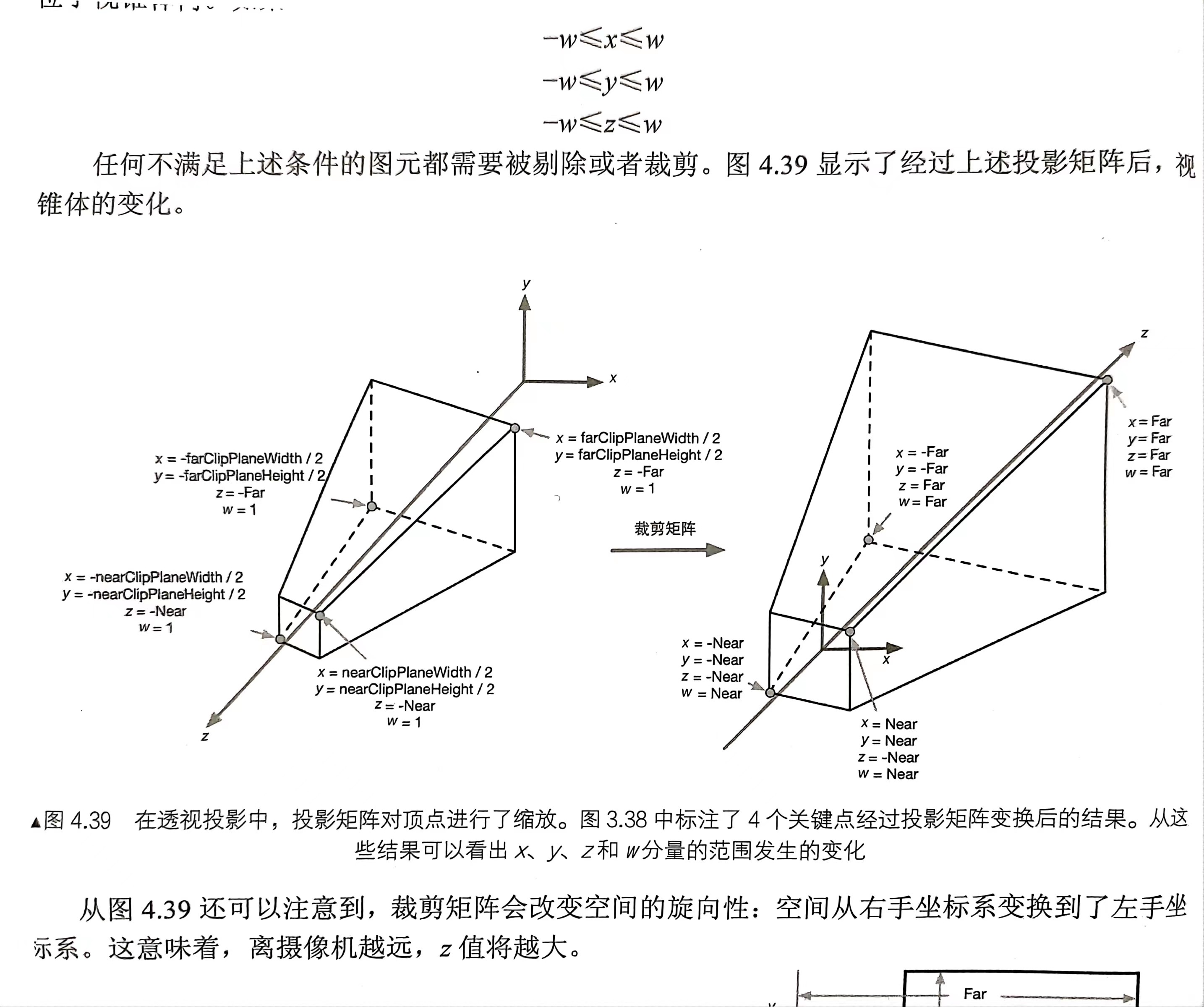
      Image

      Image

    13. **正交投影变换：**使用正交投影矩阵对顶点进行变换后，其w分量仍然为1，本质是因为投影矩阵的最后一行不同（0 0 -1 0）和（0 0 0 1）

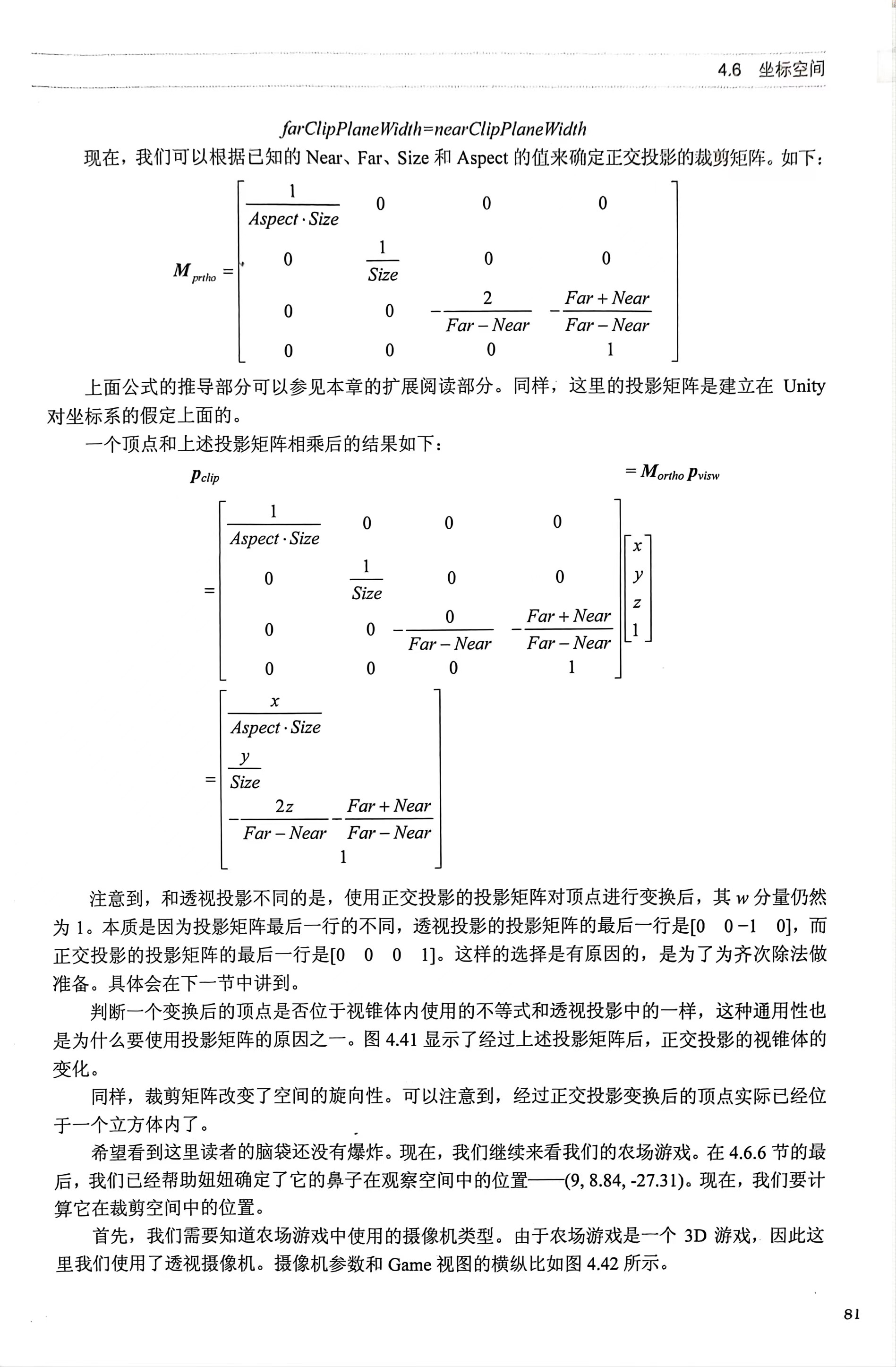
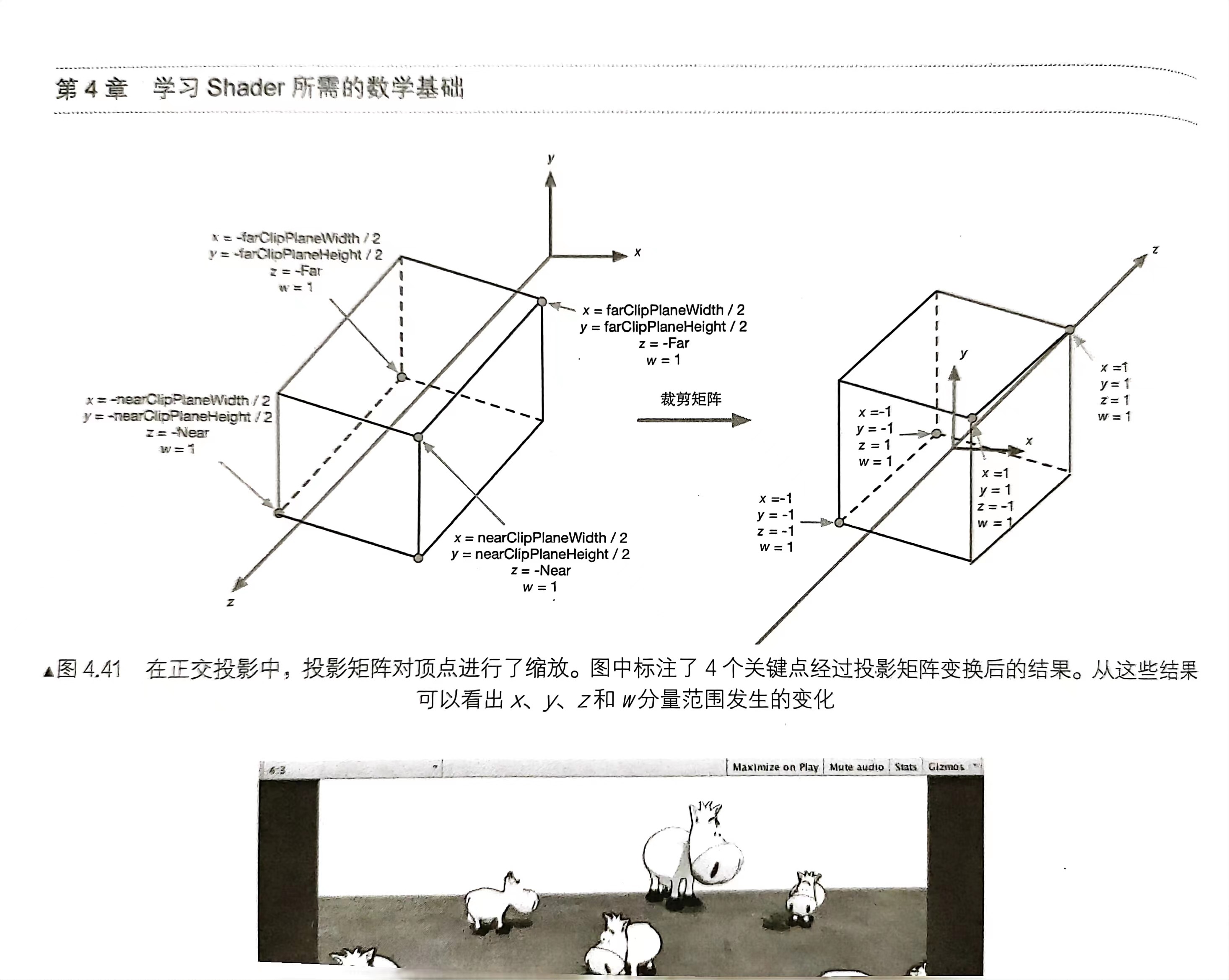
      Image

      Image

5. 法线变换

  1. 相关概念

    1. 法线（法矢量）
    2. 切线（切矢量）
    3. 法线变换：法线变换需要逆切线变换；计算的理论是切线点乘法线结果为0；**用原变化矩阵的逆转置矩阵来变换法线就可以得到正确的结果。**如果顶点的变换矩阵Mab是正交矩阵，则可以直接用Mab（T）=Mab(-1)计算得到Mab的逆转置矩阵为1/K*Mab.

    Image

    1. UNITY_MATRIX_MV如果只是进行了旋转变换，那么UNITY_MATRIX_MV是正交矩阵，UNITY_MATRIX_T_MV是其逆矩阵；

      Image

Shader基础

vert/frag基础

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
//编译指令：某个函数包含顶点，片元着色器的代码
#pragma vertex name
#pragma fragment name

// POSITION与SV_POSITION为CG/HLSL中的语义
// POSITION告诉unity把模型顶点坐标填充到v
// SV_POSITION告诉unity函数输出的是裁剪空间坐标
float4 vert(float4 v: POSITION) : SV_POSITION{
	return mul(UNITY_MATRIX_MVP, v);
}

// SV_Target告诉unity把用户输出的颜色存储到渲染目标中
fixed4 frag():SV_Target{
	return fixed4(1.0,1.0,1.0,1.0);
}

模型数据

1
2
3
4
5
6
7
8
9
10
// 定义模型数据
struct a2v{
	float4 vertex:POSITION;
	float3 normal:NORMAL; //用模型的法线方向填充normal
	float4 texcoord:TEXCOORD0; //用模型的第一套纹理填充texcoord
}

//在unity中，顶点着色器支持的输出有POSITION,TANGENT,NORMAL,TEXCOORD0-TEXCOORD3,COLOR等。
//填充到语义中的数据，由mesh render组件将其发送到unity shader。

vert/frag通信

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 使用结构体定义vert输出数据
struct v2f{
	float4 pos:SV_POSITION;
	fixed3 color:COLOR0; //COLOR0可以存储颜色信息
}

v2f vert(float4 v: POSITION) : SV_POSITION{
	v2f o;
	o.pos = mul(UNITY_MATRIX_MVP, v.vertex);
	o.color = v.normal * 0.5 + fixed(0.5,0.5,0.5);
	return o;
}
fixed4 frag(v2f i):SV_Target{
	return fixed4(i.color,1.0); //将插值后的i.color显示到屏幕上
}

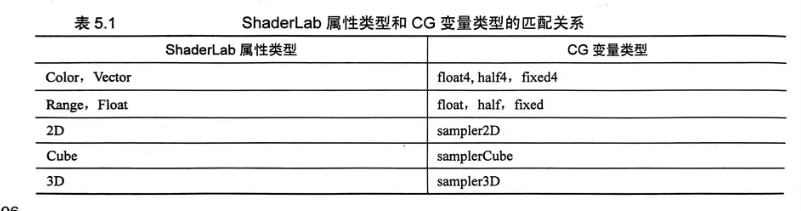
属性使用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
Shader "xxx"{
    Properties{
        _Color("Color", Color) = (1,1,1,1)
    }
    SubShader{
        Pass{
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag
            #include "UnityCG.cginc"
            //定义一个属性名称和类型都匹配的变量
            fixed4 _Color;
            struct appdata{
                float4 vertex : POSITION;
                float3 normal : NORMAL;
                float4 texcoord : TEXCOORD0;
            };
            struct v2f{
                float4 vertex : SV_POSITION;
                float4 color : COLOR0;
            };
            v2f vert(appdata v){
                v2f o;
                o.vertex = UnityObjectToClipPos(v.vertex);
                o.color = v.normal * 0.5 + fixed3(0.5,0.5,0.5);
                return o;
            }
            fixed4 frag(v2f i) : SV_Target{
                fixed3 c = i.color;
								//使用_Color属性来控制输出颜色
                c*= _Color.rgb;
                return fixed4(c,1);
            }
            ENDCG
        }
    }

}

// 也可能在CG变量前出现uniform关键字，这是修饰变量和参数的一种修饰词，仅仅用于提供关于变量的初始值是如何指定的。

Image

Unity内置文件和变量

1
2
3
4
// unity中有很多内置文件

//*********包含文件************
#include "UnityCG.cginc"

在windows中内置文件的位置如下：

部分文件是不需要include也会自动包含进来的。

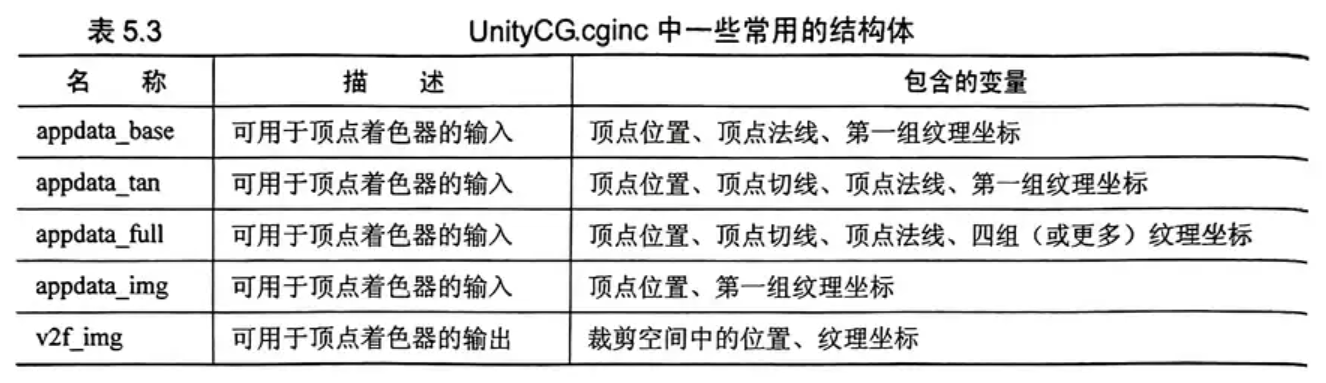
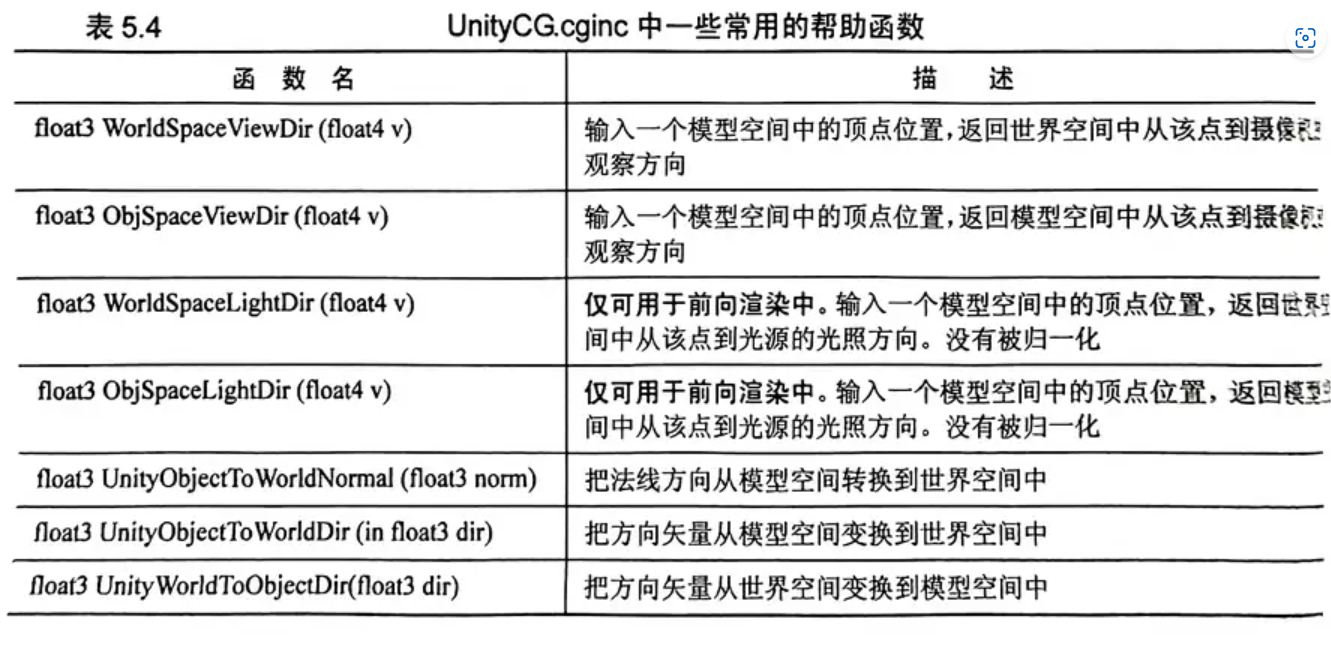
Image

Image

Image

Image

Unity提供的CG/HLSL语义

语义实际就是一个赋给shader的输入输出字符串，这个字符串表达了变量的含义。

让shader知道在哪里读数据，并把数据输出到哪里。unity没有支持所有的语义。

从DX10开始出现了一种新的语义类型，即是“系统数值语义”，以SV开头，在渲染流水线中具有特殊的含义。

用这些语义描述的变量是不可以随便赋值的，流水线需要它们来完成特定的目的。

比如渲染引擎会把SV_POSITION修饰的变量经过光栅化后显示在屏幕上。为了shader有更好的跨平台性，最好特殊含义的变量都用数值语义修饰。

一个语义可以使用的寄存器只能处理四个浮点值，对于矩阵的处理，可以进行拆分后再处理。

Shader Debug

vs种的graphics debugger可以对shader进行调试。

intel gpa，renderdoc，nvidia nsight，amd gpu perfstudio等工具都可以获得帧的信息。

unity是跨平台的，会在背后帮忙处理dx平台可能出现的纹理翻转问题，当开启抗锯齿的时候unity不会帮忙翻转纹理，此时需要手动操作。

1
2
3
4
5
#if UNITY_UV_STARTS_AT_TOP
	if(_MainTex_TexelSize.y<0){
		uv.y=1-uv.y;
	}
#endif

Image

remark: 在shader中应该慎用分支和循环语句，这样可以提高shader的性能。

同时不要在计算中出现除0，这样得到的结果是不可预测的。

Unity基础光照

  • 标准光照模型BRDF

    自发光emissive
    高光反射specular 不符合lambert定律，利用phong模型计算。blinn对该模型进行了优化，避免计算反射光线，h=（v+I）/ (v+I)，使用n和h的夹角代替计算v和r。
    漫反射diffuse 符合lambert定律，反射光线的强度和表面法线和光源方向的夹角余弦值成正比。
    环境光ambient 间接光照，相当于反射的光照

  • Cambient=gambientC_{ambient}=g_{ambient}

    Cdiffuse=(Clight∗mdiffuse)max(0,n.I)C_{diffuse}=(C_{light}*m_{diffuse})max(0,n.I) mdiffuse为漫反射颜色，需避免其余弦值为负数以防止物体被它背后的光源照亮。

    Cspecular=(Clight∗mspecular)max(0,v.r)mglassC_{specular}=(C_{light}*m_{specular})max(0,v.r)^{m_{glass}} mglass是材质的反光度，控制亮点的宽度，mpecular是高光颜色，clight是光源颜色和强度。

  • 逐像素光照与注定点光照

    在片元着色器中计算是“逐像素光照”，以像素为基础，得到它的法线（法线纹理采样/顶点法线插值计算得到）。在面片之间对顶点法线进行插值的技术被称为phong着色。

    在顶点着色器中计算是“逐顶点光照”，也叫做**高洛德着色。**在每个顶点处计算光照，然后再渲染图原内部进行线性插值，最后输出成像素颜色。

    顶点数目要远远小于像素数，所以逐顶点计算量要小于逐像素着色。但是当光照模型中有非线性的计算时，逐顶点光照计算就不适用了。